Introduction of Ellipse
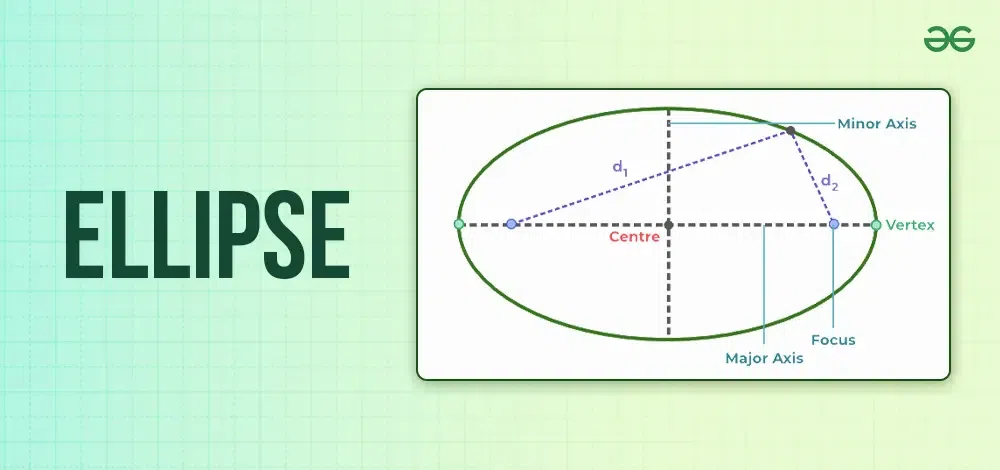
The ellipse might be one of the most interesting shapes in geometry captivating mathematicians, scientists and artists alike. An ellipse is defined to be the locus of all points in a plane such that the sum of distances from two fixed, other well-defined foci is constant: this translates into quite an unique & elegant mathematical object and it shows up everywhere across various fields (astronomy 1, architecture…)
Understanding the Ellipse
Essentially at its heart, an ellipse is a stretched circle. This has two axes), one is major axis(longer diameter) and the other minor (shortest). The separation of the foci (fixed points) defines an ellipse. The closer together these foci are, the more circular it becomes whereas when they enjoy thier distance from each other is stretched according to (elliposis).
In mathematical terms, the equation of an ellipse at origin is;
\[
x^2/a^2 + y^2/b^2 = 1
\]
In above equation, a is semi-major axis, and b is semi-minor axes.
Applications in Real Life
Ellipses are more than just lines in some drawing; they actually have real-world purposes in lots of different subject areas:
1. In astronomy the orbits of planets and satellites are frequently elliptical. Kepler’s laws 1st Law- The path of the planets are ellipses with the Sun at one focus MINI PROJECT.
2. Architectural and Engineering: Structures relying on efficient load distribution, like bridges or domes where elliptical designs are used.
3. Ellipses in Art and Architecture: Artists and architects use ellipses for both structural purposes and aesthetic reasons. An example of elliptical architecture: the celebrated dome of St. Peter’s Basilica in Vatican City
Sound response: Ellipses behave differently for sound. They can be used for artistic effect in some churches but are difficult to install because the doubly curved mylar surface must have special limit curves or they will pucker; this is another form of conic sections where parabolas, circles and ellipses with both focal points at one focus become self-sustaining when flown out from that room loudspeaker.
4. Ellipsis in Nature
Aside from man-made applications, nature is a common place to find ellipses. There are some fruits that show elliptical shapes, the trails of comets and also how certain moons orbit around planets. This natural display of ellipses highlights just how perfect and thouroughly used this simple geometric shape can be.
Conclusion
It speaks to the very core of our understanding of mathematics, science, art and nature. It is interesting and a subject of research investigation due to its unique characteristics, as well very broad applications. Whether in the sky, or here on Earth: ellipses remind us of all the intricate elegance that surrounds. The more we explore and comprehend this shape, the deeper insights it reveals into our universe’s patterns and relationships